Alex Rich
I'm a PhD student in computer science at UCSB, advised by Tobias Höllerer. I am broadly interested in machine learning, computer vision, and computer graphics. My research focuses on multi-view stereo and 3D reconstruction, with many applications including augmented and virtual reality, and autonomous navigation.
During my PhD, I interned with Apple's VIO/Slam group, working on IMU-only navigation with Stergios Roumeliotis. Prior to my PhD, I was a software engineer at Apeel Sciences.
I earned a B.S. from UCSB in mathematics, where I worked with Kenneth C. Millett on knot theory and the analysis of common subknots in minimal prime knot presentations.
Alex Rich, Noah Stier, Pradeep Sen, Tobias Höllerer
ECCV 2024 (Oral Presentation)
project page / PDF / code
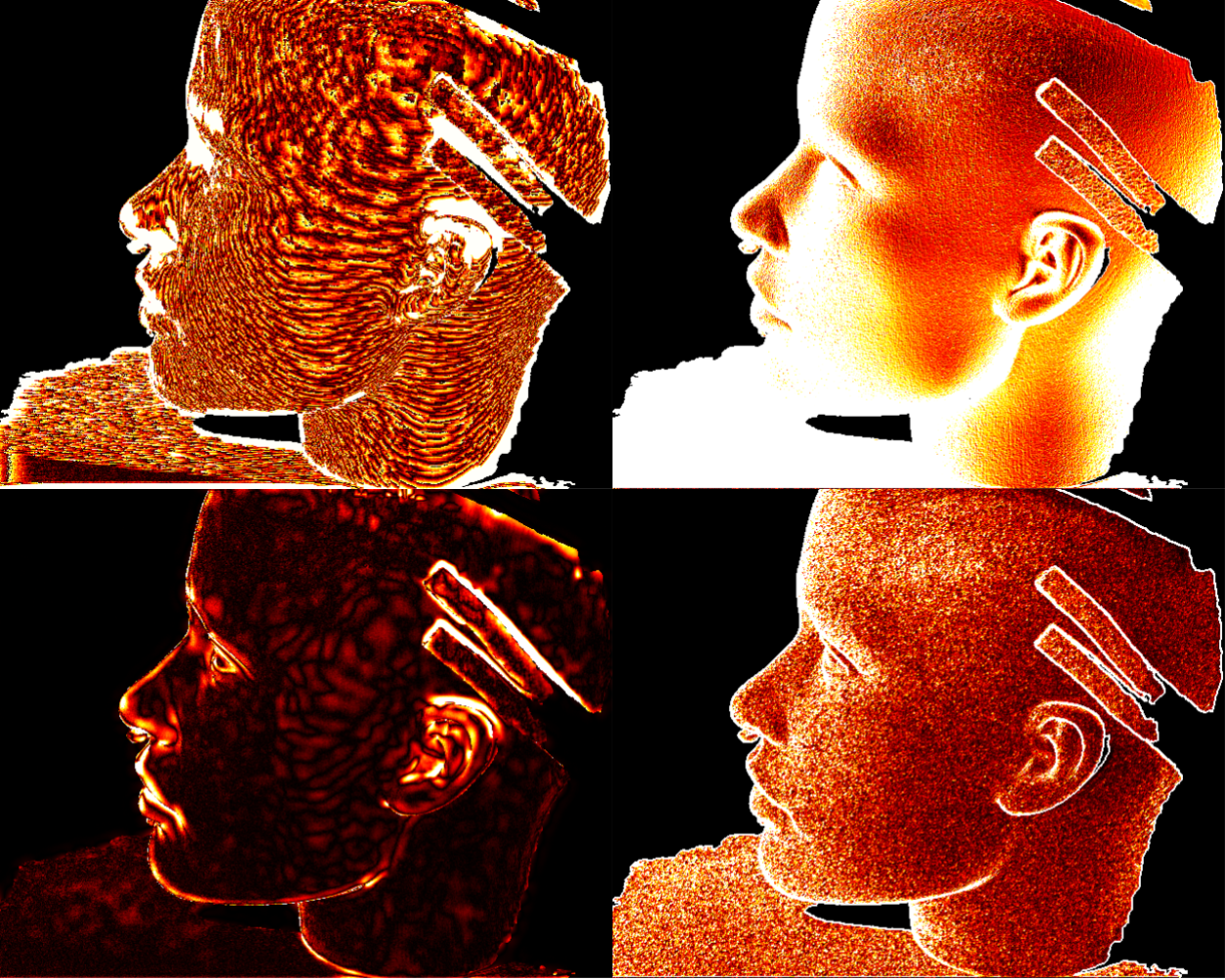
We introduce DIV Loss, a novel loss formulation for unsupservised multi-view stereo. The key advantage of our DIV loss is that it can be easily dropped into existing unsupervised MVS training pipelines, resulting in significant quantitative and qualitative improvements.

Alexander Rich, Noah Stier, Pradeep Sen, Tobias Höllerer
3DV 2021
project page / arXiv / code
We introduce a deep multi-view stereo network that jointly models all depth maps in scene space, allowing it to learn geometric priors across entire scenes. It iteratively refines its predictions, leading to highly coherent reconstructions.

Noah Stier, Alexander Rich, Pradeep Sen, Tobias Höllerer
3DV 2021 (Oral Presentation)
arXiv / code
We introduce a 3D reconstruction model with a novel multi-view fusion method based on transformers. It models occlusion by predicting projective occupancy, which reduces noise and leads to more detailed and complete reconstructions.

Pranav Acharya, Daniel Lohn, Vivian Ross, Maya Ha, Alexander Rich, Ehsan Sayyad, Tobias Höllerer
ILDAV Workshop, Adjunct Proceedings of ICCV 2021
PDF / code
We introduce a synthetic data generation pipeline, which produces image sequences for multi-view stereo methods given 3D scene models as input. We utilize this pipeline to study existing multi-view-stereo depth-prediction methods. Among other results, we find that camera height and vertical camera viewing angle are the parameters that cause the most variation in depth-prediction errors on these image sequences.
Kento Nishi, Yi Ding, Alex Rich, Tobias Höllerer
CVPR 2020
arXiv / code
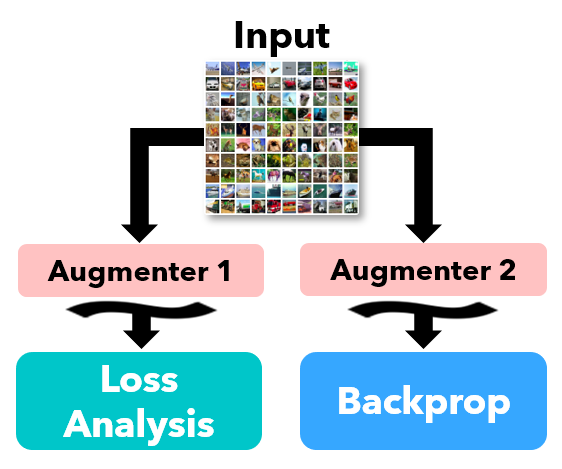
We propose Augmented Descent, a data augmentation strategy for training deep classifiers robust to incorrect labels in the training set. This technique works by using one set of augmentations for loss modeling tasks common to existing noise-robust training methods, while using a separate set of augmentations for backpropagation.
Kenneth C. Millett, Alex Rich
Journal of Knot Theory and its Ramifications 2017
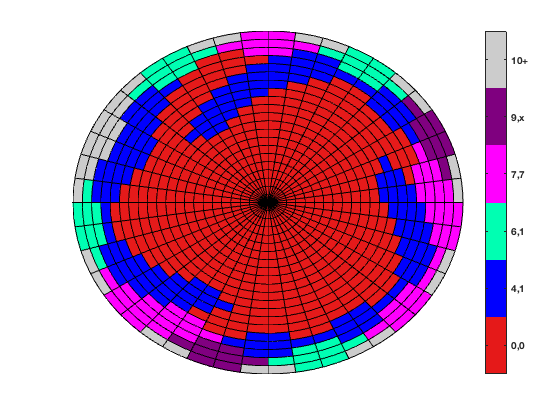
We perform a comprehensive study of subknots in minimal prime knot presentations through 15 crossings. We find among this set of 313,258 prime knot presentations, 99.83% contain a trefoil subknot and every knot contains either a trefoil subknot or a figure-eight subknot.
Website design from Jon Barron.
